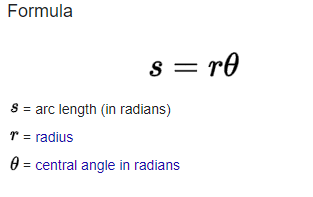Simplify your curved shape measurements with our Arc Length Calculator. Just input the details, and it quickly gives you the length of the arc, making geometry calculations easy and accurate.
RESULTS
Calculating the precise length of an arc can be difficult, especially when dealing with complex geometrical figures. A reliable tool like the Arc Length Calculator is essential for those in fields requiring exact measurements.
Our guide will explore the functionalities of this calculator, simplifying intricate computations into a few clicks. With our helpful insights, you’ll conquer mathematical barriers and achieve accurate results effortlessly.
The Arc Length Calculator
The Arc Length Calculator stands as a precise digital tool designed to effortlessly compute various geometrical parameters, including the elusive arc length. Seamlessly transforming input data into accurate results, this calculator simplifies complex calculations in a user-friendly interface conducive to both educational and professional environments.
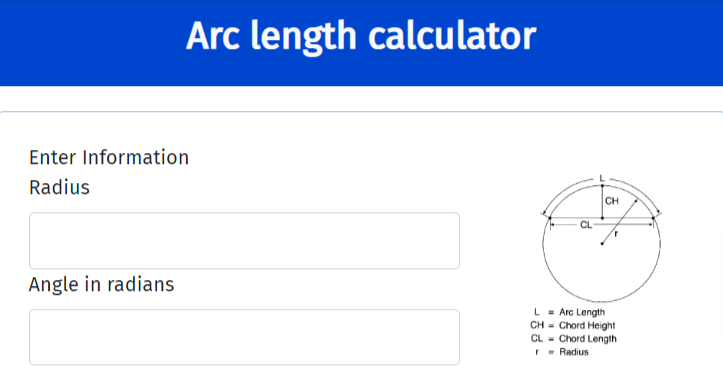
Input parameters and values
Arc-length calculators are great tools for math and science. They help you find the size of a curve quickly and easily. Here’s how you can use one:
- Choose what you need to calculate: You can pick from central angle and radius, radius and segment height, or many other combinations.
- Enter the numbers: After selecting your calculation type, type in the values for each parameter.
- Pick units: Decide if you want your answer in inches, centimeters, feet, meters, or another unit.
- Get results fast: Once all information is in, the calculator does its magic and shows you the arc length plus other helpful info like diameter or area.
Calculation of arc length, diameter, area, radius, central angle, segment height, and chord
Once you put in the numbers, the calculator gets to work on finding not just the arc length but also other key parts of a circle. You can figure out how big a circle is, how wide it is across the middle, what its radius is, and more.
The tool makes it easy to find these details with just a few clicks. It uses formulas like “s = ϴ × r” when you measure angles in radians or “s = 2 π r (θ/360°)” if you use degrees.
This smart calculator can help with many kinds of problems. Need to know how tall a segment stands? Just type in what you know about your circle’s sector or chord. Or perhaps you’re working on something bigger and need to know the area inside that curve—a task this nifty gadget handles without fuss.
Whether it’s sharp angles or smooth lines between two points, this calculator turns complex math into simple answers fast!
- Common Angle Conversions:
| Degrees (°) | Radians (rad) |
|---|---|
| 0° | 0 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
Selection of units of measurements
Choosing the right units for measuring is important when using an arc length calculator. You might need to use inches, centimeters, or even millimeters based on what you are working on.
The same goes for calculating areas and lengths. You can pick from square inches or square centimeters if you’re looking at area, or maybe meters if you’re measuring a longer distance.
The calculator lets you easily switch between different units so your numbers make sense for your project. For angles, you may need degrees or radians depending on your math problem.
This flexibility makes sure that all of your measurements fit together nicely and helps you solve problems accurately without any mix-ups. You can also solve for the length of the sides of a right triangle using our Pythagorean Theorem Calculator.
The Formula for Arc Length
Understanding the precise formula for calculating arc length is crucial, as it serves as the foundation for accurately measuring curved distances within various sectors of a circle; continue reading to uncover its intricacies and practical applications in numerous fields.
s = ϴ × r for radians
To find out how long a piece of a circle’s edge is, we use the arc length formula s = ϴ × r. This works when you measure the slice of the circle in radians. Imagine drawing a straight line from the center of a pizza to the crust – that’s your radius (r).
Next, look at how wide your pizza slice is – that’s your angle (ϴ), but it has to be in radians for this magic formula to work right.
Think about using this simple rule next time you need to figure out an arc’s size on any circle. It’s super useful for math problems and lots more – like building things or understanding space! All you have to do is multiply two numbers: the radius and the radian measure of your central angle.
Just like that, you have your arc length! It might sound tricky with words like “radians” and “radius,” but once you try it, it makes perfect sense.
s = 2 π r (θ/360°) for degrees
When you want to find out how long an arc is, and you have the angle in degrees, this formula works like magic. You take that angle and divide it by 360°. Why 360°? Because that’s how many degrees are in a full circle! Next, multiply your answer with 2 π (pi), which is about 3.14.
Now take the circle’s radius – the distance from the center to the edge – and multiply that by your first answer. That number you get is your arc length!
Let’s say you’re working on a project where precision matters. You wouldn’t want to guess or be off even by a little bit, right? With this formula, you can be sure about the measurement of any part of a circle’s edge between two points—the arc length you’re looking for! It’s important for making things fit together perfectly, whether it’s parts of machines or pieces of art that need curves just right.
Use these steps with care to get accurate results every single time.
Solved example demonstration
Let’s look at a real example to see our arc length calculator in action. Imagine you have a slice of pizza that is part of a larger 14-inch pie, and the tip of your slice makes a 60-degree angle from the center.
You want to know how long the crust is along the edge of your slice.
First, you enter the radius (7 inches since it’s half of 14 inches) and select degrees as your unit for measuring angles. Then type “60” into the central angle box. The calculator instantly works out that your crust – or arc length – is about 7.33 inches long! This quick example shows exactly how useful the calculator can be for all sorts of problems involving circles.
Now imagine using this tool in complex designs or astronomy calculations; you’ll quickly find how vital an accurate arc length measurement can be! And we’ve only just touched on one aspect – there’s also diameter, sector area, and more that it can calculate for you. Now you can also calculate the volume, surface area, and other properties of a sphere with our comprehensive Sphere Calculator.
Benefits of the Arc Length Calculator
The Arc Length Calculator stands as an indispensable tool, streamlining computations with unmatched precision and simplifying complex geometrical tasks. Its user-centric design facilitates seamless conversion across various units, ensuring its utility extends from academic classrooms to the intricate demands of professional fields.
Accuracy in calculating arc length
Getting the arc length right matters a lot, especially in fields like engineering and astronomy. Using an arc length calculator helps you find this important number without mistakes.
You just type in what you know—like radius and angle—and it works out the arc length for you. It’s really precise because it uses tested formulas for its math.
With this tool, anyone can be sure to get exact numbers every time, no matter if they’re working with radians or degrees. And that means less stress about getting things wrong and more trust in your final answers.
This makes projects smoother because accurate measurements guide good decisions along the way.
Ease of use for different measurements
The Arc Length Calculator makes working with different measurements simple. You can pick from many units like inches, centimeters, or meters to get your results the way you need them.
Just type in what you know about the circle, like the radius or angle, and choose your preferred unit. The calculator does all the hard math for you.
It’s great for people who use these calculations at work or school because it saves time and helps avoid mistakes. Next, let’s explore how knowing the right formula makes finding arc lengths even easier.
Applicability in various fields such as science, engineering, and astronomy
Scientists, engineers, and astronomers often need to measure curves and circles. They use arc-length calculators for this work. For example, in astronomy, they may calculate the path of a planet or star.
Engineers might need it to design parts that curve. In science classrooms, teachers show how to find the size of arcs in experiments.
This tool helps to get answers quickly and right. It lets users pick different units like meters or inches for their measurements. Users can easily add this calculator to their own websites too.
Now let’s look more at the formula used in an arc length calculator. You can also determine the arcsin (inverse sine) of a value effortlessly using our Arcsin Calculator.
FAQs
1. Does an arc length calculator work with different shapes?
Sure does! It can handle circles and other curves like ellipses or heart-shaped cardioid figures by using math rules for those shapes.
2. Is an arc length only used in flat shapes?
Nope! Arc lengths are also important when you deal with 3D stuff like balls or tubes, known as solids of revolution because they spin around to make their shapes.
3. Do I need to know special math terms to use it?
Not really. The calculator uses things like radii (the spokes from center to edge), sine functions (a wave pattern), and coordinates (spots marked on graphs) but it does most of this for you.
4. Is the Arc Length Calculator applicable to 3D geometry or only 2D circles?
The calculator focuses on 2D circles. For 3D geometry involving spheres, specific formulas would apply, and our calculator is not tailored for such scenarios.
5. How does the Arc Length Calculator contribute to real-world applications?
From constructing circular structures to optimizing paths, our calculator aids in real-world scenarios requiring accurate arc length calculations, contributing to efficient designs and projects.
Related Calculators: