Try our Pythagorean Theorem Calculator for quick and accurate triangle calculations. Its user-friendly interface and wide range of applications make it a valuable tool for students, engineers, and professionals.
RESULTS
Struggling to solve right triangles in your math homework? The Pythagorean Theorem, a cornerstone of geometry, describes the relationship between the sides of these angles. Our guide will help you with complex calculations.
Understanding the Pythagorean Theorem
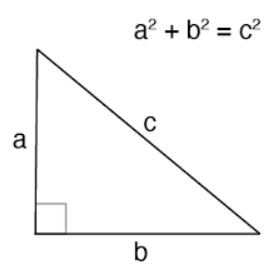
The Pythagorean Theorem is a fundamental principle in geometry. It describes a special relationship between the sides of a right triangle. The theorem states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is named after the ancient Greek mathematician Pythagoras, although it was known and used by many cultures before him. It’s a fundamental tool in many areas of mathematics and physics, including geometry, trigonometry, and even Einstein’s theory of relativity.
The formula for solving for side a, side b, hypotenuse c, and area A
You can find out the length of any side in a right triangle with the Pythagorean theorem. If you know the hypotenuse and one side, use a = √(c^2 – b^2) to get the other side. Or, if you have both sides but need the hypotenuse, c = √(a^2 + b^2) tells you its length.
To figure out how much space that triangle takes up, multiply half of one side by another using A = 1/2ab.
These formulas help solve many real-world problems. Imagine setting up a ladder or checking a map; they are your tools for measuring things that form right angles. Next, let’s see how our calculator makes these math tasks even easier!
The Pythagorean theorem formula: c^2 = a^2 + b^2
The Pythagorean theorem formula is a way to find the length of the longest side in a right triangle, which we call the hypotenuse. It says that if you square both of the other sides, called ‘a’ and ‘b’, and add those numbers together, it will equal the square of the hypotenuse ‘c’.
In math, this is written as c^2 = a^2 + b^2. This rule helps people figure out distance and sizes without having to measure directly. For calculating distance you can use our distance calculator.
Working with this formula can solve many problems. Use these two measurements as sides ‘a’ and ‘b’. With them, you can calculate side ‘c’.
How the Pythagorean Theorem Calculator Works
The Pythagorean Theorem Calculator simplifies complex calculations, providing a user-friendly interface where you can swiftly enter known values to determine the missing side of a right triangle.
With just a few clicks, you will receive a detailed step-by-step guide that gives you the answer and helps you understand this fundamental geometric principle.
Inputting the known values and selecting units and decimal places
To use the Pythagorean theorem calculator, start by filling in the lengths you know. For example, if you have a right triangle and you know two sides, put those numbers in. Make sure to pick the correct measurement unit for your problem—meters, centimeters, inches or others.
Also, choose how many decimal places you want the answer to have.
This calculator makes it easy to get precise answers. If you’re only given one side and need the other or even if you’re looking for how big an area is, simply input what you know.
Select from options like millimeters or feet, then decide whether your answer should be rounded to one place or maybe even four. You get control over these choices so your calculations fit your needs perfectly! You can also check our arc length calculator for calculating the length of the arc.
Applications of the Pythagorean Theorem
The Pythagorean Theorem goes beyond mere geometry, proving invaluable in diverse fields such as construction and navigation—discover how this ancient principle remains crucial to modern problem-solving.
Real-life scenarios such as finding the length of a ladder
Imagine you need to reach the top of a wall or building. You have a ladder, but you’re not sure if it’s long enough to be safe and stable. This is where the Pythagorean theorem helps out! It tells us how long the ladder needs to be when leaning against a wall at a right angle.
With this math tool, you plug in the height of the wall and how far away from it you want your ladder base to be. It calculates the perfect ladder length for you. It ensures that professionals like firefighters or painters can work safely every day. Plus, anyone at home doing repairs can make sure they’re climbing securely too.
Pythagorean Triples and Their Application
These mathematical methods not only simplify computations but also help you with practical applications, from architecture to navigation, by offering consistent solutions to common geometric problems.
Sets of three positive integers (a, b, c) that satisfy the equation a^2 + b^2 = c^2
Pythagorean triples are trio numbers. They fit perfectly into the Pythagorean equation a² + b² = c². Each number in the set is a whole number, and when you square two of them and add those squares together, you get the third one squared.
It’s like they were made for each other! This math trick helps people solve problems with right triangles.
One famous set of these numbers is 3, 4, and 5. If you take 3 times itself (which is 9) and add it to 4 times itself (which is 16), their sum equals 5 times itself (25). These special sets make working with triangles much easier because you don’t have to measure every time—you just use these handy groups of three numbers that already fit the rule. That way, you can find side lengths fast and get on with building things or solving puzzles that need the right angles. For calculating square footage area you can use our square footage calculator.
Validity and Reliability of the Pythagorean Theorem
While the Pythagorean Theorem is a steadfast rule in geometry for right-angled triangles, there are conditions and geometries where it does not apply. Understanding this theorem’s limitations is crucial for its proper application across different mathematical contexts.
Conditions under which the theorem may not hold true
Sometimes the Pythagorean theorem doesn’t work. It’s made for right triangles only. If a triangle has an angle bigger than 90 degrees, which is an obtuse triangle, or all angles less than 90 degrees, called an acute triangle, this rule does not apply.
Also, the sides must make sense together; if any two sides added up are not longer than the third side, you can’t have a real triangle.
Let’s say we try to use it on shapes that aren’t even triangles. For example, in four-sided squares or five-sided pentagons, this math trick won’t help us find their sides because they don’t fit the rules of having one right angle and three sides only.
We need other ways to solve these problems! Remembering where and how we can use Pythagoras helps us do math better.
Here are a couple of tables related to Pythagoras’ theorem:
1.Pythagorean Triples Table:
A Pythagorean triple consists of three positive integers, a, and c, such that 2+2= 2. Here’s a table showing some Pythagorean triples:
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 8 | 15 | 17 |
| 9 | 40 | 41 |
| 11 | 60 | 61 |
| 12 | 35 | 37 |
| 13 | 84 | 85 |
| 15 | 112 | 113 |
- Sides of a Right Triangle:
Given two sides of a right triangle, you can use Pythagoras’ theorem to find the length of the third side. Here’s a table showing how Pythagoras’ theorem can be used:
| 3 | 4 | 5 |
| 6 | 8 | 10 |
| 5 | 12 | 13 |
| 8 | 15 | 17 |
| 12 | 9 | 15 |
In this table, and are the lengths of the legs of the right triangle, and is the length of the hypotenuse, calculated using
FAQs
1. Why use a Pythagorean Theorem calculator with variables?
A calculator with variables allows you to find any unknown side of a right triangle. Whether you know the hypotenuse and one leg, or both legs but not the hypotenuse, a calculator with variables can provide the answer.
2. Can this calculator work with areas and angles too?
Yes, it can help you understand areas of squares on triangle sides and use trigonometric functions like sine and cosine to deal with angles.
3. How does the Pythagorean Theory help me in math?
The Pythagorean Theory tells you how sides in a right-angle triangle relate to each other which helps solve problems about distance and more.
4. Is the Pythagorean Theorem only for flat shapes?
No, it also works for three-dimensional space by applying its generalization or using related theories like the law of cosines.
5. Did only Pythagoras know about this theorem?
No, even before the Greek mathematician Pythagoras, people like Babylonians knew about special cases of these triangles and their properties.
6. Can I learn about complex numbers with this theory?
Yes! While complex numbers don’t fit directly into the traditional Pythagorean formula, concepts from a cartesian coordinate plane are used to explore them further.
Related Calculators: