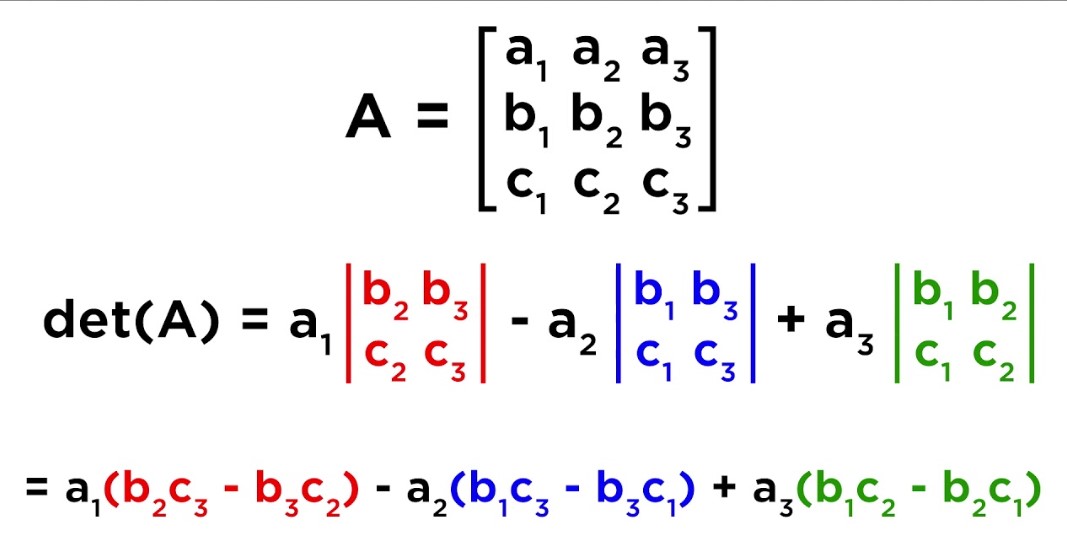Try our cross product calculator for quick and accurate results with 2D and 3D vectors. It offers a user friendly interface and is useful for various fields such as physics, engineering, and mathematics.
RESULTS
Calculating the cross product of two vectors can be a daunting task, especially if you’re not familiar with vector math. A key aspect of vectors in three dimensional space is their ability to model forces and directions accurately.
With our cross product calculator, finding the vector perpendicular to your original pair becomes easy. This tool provides clear guidance for anyone looking to conquer this fundamental concept in physics and engineering.
Understanding the Cross Product of Vectors
Understanding the cross product of vectors is necessary in understanding many physical concepts and applications ranging from rotational dynamics to electromagnetic effects. This operation, unlike simple arithmetic, involves both magnitude and direction, yielding a vector that is orthogonal to the plane formed by the two original vectors.
Definition of the cross product
The cross product is a special way to multiply two vectors in three dimensions. It’s different from the dot product or scalar product, which gives you a single number. When you do a cross product, the answer is another vector! This new vector is at right angles to the original two vectors.
People use it in physics and engineering to figure out things like force on an object moving through a magnetic field.
For example, if you have one vector pointing straight up and another going forward, their cross product points either left or right—imagine it as telling us about how they spin around each other.
The direction of this new side to side vector depends on something called the “right hand rule”, where your fingers show how the first vector goes into the second one and your thumb points outwards in the direction of our answer vector. Discover the power of precision with our Pythagorean Theorem Calculator! Simplify your geometry and calculate side lengths effortlessly.
Calculation formula
Understanding the cross product means we can now dive into how to calculate it. The formula might look a bit tough, but once you get the hang of it, it’s like solving a puzzle! You take two vectors and use them to make a third one that is at right angles to both.
Here’s what you do: write down the unit vectors for X, Y, and Z axes. Then list the numbers from your first vector and your second vector underneath. After this setup, you find the difference between certain products of these numbers.
For example, multiply some of the numbers from each vector in a crisscross way kind of like an “X.” But remember there’s also subtraction involved! You will subtract one product from another to get each part of your new vector.
It’s important because this tells us about things like torque or magnetic forces in 3D space!
One more thing about calculating cross products, they help us know if things are moving forwards or spinning around. Just type in your numbers into our calculator and watch as it does all this cool math for you step by step. No need for paper or pencils; let technology make finding cross products easy as pie!
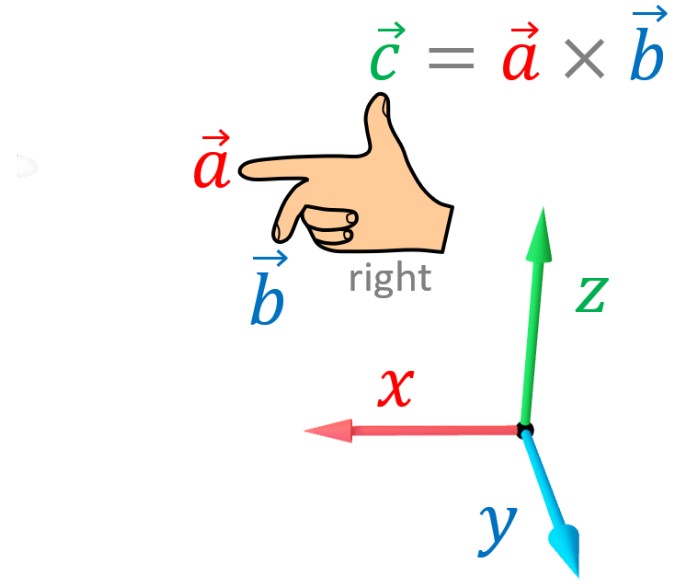
Right hand rule
Now that we know the formula, let’s explore how to figure out the direction of our cross product with the right hand rule. Picture your right hand in front of you. Point your pointer finger straight ahead; this will be your first vector (A).
Now, stick out your middle finger at a right angle to your pointer; this is going to be your second vector (B). Then, point your thumb up—that’s where the cross product points (C).
It may feel like magic, but it’s all about using your fingers to see which way things go! This trick helps people working with magnetism and motors make sure they get their directions just right.
The best part is that you can use this rule every time you work with vectors in three dimensions. If you need to find out where a spinning wheel will push air or which way an electric current makes magnets move, just call on the handy dandy right hand rule.
Keep practicing by trying it out next time you’re doing physics problems or when using our online calculator for quick and accurate answers! Master modular arithmetic effortlessly! Optimize your calculations with our Modulo Calculator.
The Cross Product Calculator
The Cross Product Calculator is a helpful tool that simplifies the computation of vector cross products. It provides a precise and straightforward platform, suitable for both students and professionals.
With its advanced functionality, users can effortlessly input their vector parameters, engage with a user friendly interface, and receive accurate step by step solutions, transforming complex calculations into manageable tasks.
Step by step calculations
Calculating the cross product of two vectors is key in many fields like physics and engineering. Our Cross Product Calculator makes this complex task simple and quick. Here’s how you can do it step by step:
- First, write down your vectors. You’ll have two of them, each with three parts: the x, y, and z components.
- Now, look at our calculator. There’s a space for each part of your vectors.
- Put the x component of your first vector in the first box.
- Enter the y component of your first vector next.
- Fill in the z component of your first vector into its spot.
- Do the same for your second vector: x goes into its box, then y, and finally z.
- Check everything to make sure you entered all numbers correctly.
- Click on the button that says “Calculate.” It does all the hard work for you!
- After a moment, see your answer! The calculator shows a new vector with x, y, and z parts.
User friendly interface
Our Cross Product Calculator is designed with you in mind. It’s easy to see where to enter your vector information and the layout makes sure you don’t get lost. All the buttons are clear, and the screen isn’t cluttered with too many things at once.
This means you can focus on getting your cross product without any stress.
The calculator not only looks good but works smoothly too. You click, type in your numbers for each vector, and let it do its magic. It shows your answer fast so that you can move on to what’s next quickly – like using those results for more math problems or applying them to real world situations in physics or engineering.
Now, let’s look at how to use this handy tool efficiently.
Input parameters for vectors
The calculator is built to be easy to use. You need some info from your vectors to start. For two vectors, you give the calculator three numbers for each one. These are like steps that show how far the vector goes in the direction of the x-axis (left or right), y-axis (up or down), and z-axis (forward or back).
This way, it has all it needs to do its job.
You type these numbers into boxes on the screen. The first box gets the numbers for going left or right, called ‘X’. The next box gets ‘Y’ for up or down moves. And ‘Z’ goes last, for forward and backward steps.
Make sure you put them in just as they are so everything works out right. Discover the arc length effortlessly, try our Arc Length Calculator now for accurate results and elevate your geometric insights!
How to Use the Cross Product Calculator
How to Use the Cross Product Calculator: Seamlessly compute the cross product of two vectors using our intuitive tool, simplifying complex operations into clear, manageable results—empower your vector calculations by exploring further.
Input vector parameters
Input vector parameters are important for finding the cross product. Our Cross Product Calculator makes it easy to enter these values. Here’s what you need to do:
- Choose the space where your vectors exist. Most of the time, you’ll work in three dimensional space.
- Enter the first vector’s components in the fields labelled ‘Vector A.’ These could be numbers like ‘3,’ ‘4,’ or ‘5.’
- Fill in the second vector’s components under ‘Vector B.’ Make sure these are also numbers and that they match up with the first vector’s dimensions.
- Take care to input each number in its correct place. This means if ‘X’ is first for Vector A, put ‘X’ first for Vector B too.
Determine unit vector coefficients
After you have put in your vector values, the next step is to figure out the unit vector coefficients. These are numbers that show the direction of a vector. They make up a part of the cross product formula. Here’s how you can find them:
- First, write down your full vectors. Let’s say Vector A has x, y, and z parts, and so does Vector B.
- Next, look at the x part of Vector A. Multiply it by the y and z parts of Vector B. But don’t mix up the order.
- Now do this for the y part of Vector A too. You’ll need to use both x and z from Vector B.
- Don’t forget about z from Vector A! It also gets multiplied with x and y from Vector B.
- Okay, watch out for minus signs! Sometimes when you switch parts around, you need to change plus to minus or minus to plus.
- Keep doing these steps until you have three new numbers, one for each part (x,y,z) of your new cross product.
Calculation steps
Once you know the unit vector coefficients, you can move on to calculate the cross product. Here’s how to do it step by step:
Example
You put together your two vectors in rows and add one more row with symbols i, j, and k on top. These are not numbers but special signs that help you keep track of directions.
You then draw lines to multiply across and down, like playing connect-the-dots with math. This setup is your secret map to finding out how the three vectors work together in space.
It’s neat because it shows you all the possible ways they can mix and match their parts! Simplify quadratic equations effortlessly! Optimize your math with our Quadratic Formula Calculator.
Calculating the determinant
Calculating the determinant helps you find the cross product of two vectors. This math step is key in many areas, like physics and engineering.
- First, write down your vectors in a grid called a matrix.
- Your matrix should have three rows and three columns.
- In the top row, put the unit vectors i, j, k.
- In the middle row, enter the components of your first vector.
- Put your second vector’s components in the bottom row.
- Now, cover up the first column and first row. You will see a smaller square.
- Multiply its top left number by its bottom right number.
- Next, multiply its top right number by its bottom left number.
- Subtract the second product from the first one you found. Write this number down.
- Cover up each column (one at a time) that has an i, j, or k at the top.
- Use the numbers in each small square like before: multiply across and then subtract.
FAQs
1. Is the calculator suitable for engineering applications?
Yes, it’s ideal for engineering. Input vectors representing forces or velocities, and the calculator computes the cross product, crucial for applications like determining moments and calculating magnetic flux in electrical systems.
2. How can the Cross Product Calculator assist in geometric calculations?
For geometric problems, input vectors representing sides or diagonals of polygons, and the calculator computes the cross product, aiding in calculations of area, orientation, and angles.
3. Can I use a calculator for electromagnetism problems?
Yes, in electromagnetism, calculators can do binary operations like finding magnetic moments and acceleration by measuring angles and applying the distributive law.
4. Why is it important to know about scalar and dot products too?
Knowing about scalar and dot products matters because they are different kinds of multiplications used along with cross products to solve physics problems involving motion, like moment of inertia or orientation changes.
5. What’s special about vectors in quantum field theory?
Vectors in quantum field theory are very important because they represent quantities that have direction and size; this helps scientists understand things like fields and forces better.
6. Does linear independence relate to finding cross products?
Yes! When two vectors are linearly independent, their cross product tells us if they point in random directions or not; this also checks if we can use them together mathematically for complex calculations.
7. Does the Cross Product Calculator support symbolic input for mathematical expressions?
No, the calculator currently accepts numerical input for vectors. It performs computations based on the numeric values of the input vectors rather than symbolic expressions.
Related Calculators: