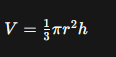Effortlessly compute cone volumes with our Cone Volume Calculator. Simplify geometric calculations and ensure precision in determining the volume of cones for various applications.
RESULTS
Struggling to figure out how much your cone-shaped cup can hold? You’re not alone, as calculating the volume of a cone can be quite tricky.
This guide will help you use this handy device to solve your volume problems effortlessly. Get ready for clarity!
Understanding Cones and Their Volume
Formula For Cone Volume
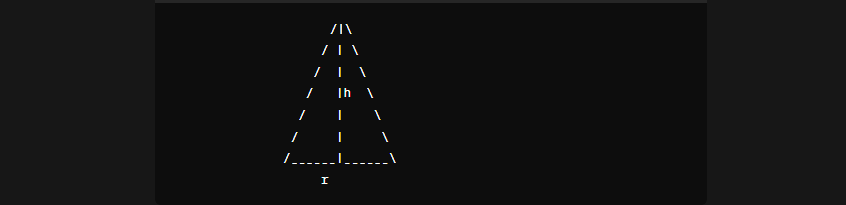
To find the volume of a cone, use this simple formula: V = (1/3)πr^2h. Here, V stands for the volume you want to figure out. The letter r is the radius of the circular base, and h is how tall the cone is.
This easy equation tells you how much space there is inside a cone.
You get this handy formula from thinking about cylinders. A cone’s volume is just one-third of what cylinders would be if they both had the same height and round bottom size. Keep in mind that π (pi) roughly equals 3.14159, but your calculator can handle that part!
Where:
- is the volume of the cone
- is the radius of the base of the cone
- ℎ is the height of the cone
- is a mathematical constant approximately equal to 3.14159
Now, let’s represent this formula graphically:
In this diagram:
- represents the radius of the base of the cone.
- ℎ represents the height of the cone.
- represents the volume of the cone.
The volume of the cone is calculated by taking one-third of the area of the base ((1/3)πr²) and multiplying it by the height (ℎ). This gives us the volume enclosed by the cone. Also, Try our Arc Length Calculator to find the length of an arc.
Types Of Cones
we categorize cones based on their symmetry and axis — each with distinct characteristics influencing their volume calculations. Understanding these variations is pivotal as they underpin many practical applications from engineering to everyday life.
Right Circular Cone
A right circular cone stands tall with its point, or apex, directly above its base’s center. This type of cone has a smooth surface that curves from the base to the apex. Imagine an ice cream cone or a party hat; these are everyday items shaped like a circular cone.
To determine how much space is inside this cone, you can use a simple math formula: V = (1/3)πr²h. For this calculation, r represents the radius of the wide end—the base—and h is how high the cone reaches from base to tip.
These measurements help engineers and builders easily figure out volumes for things like funnels and traffic cones.
Oblique Cone
An oblique cone stands out because one side is tilted and the point is not above the center of the base. This tilt doesn’t change how you find its volume. Imagine pouring water into a slanted glass – it can hold as much liquid as a straight one if they are the same size.
You still use V = (1/3)πr^2h to figure out how much space it has inside. The “r” measures across the circular bottom, while the “h” is from base to tip along the edge.
Moving forward, let’s explore another type of cone – the truncated cone or frustum.
Truncated Cone (Frustum)
Moving from oblique cones to truncated cones, we enter the world of frustums. A truncated cone, or a frustum, has its top sliced off with a cut parallel to the base. This creates two circular bases of different sizes.
To find out how much space this shape takes up, you can use a special formula: V = (1/3)πh(R^2 + r^2 + Rr). Here, ‘V’ stands for volume, ‘h’ is the height between the two bases, and R and r are the radii of the larger and smaller circles at each end.
Calculating surface area requires another formula: A = π(R + r)l + π(R^2 + r^2), where ‘A’ represents the surface area and ‘l’ is the slant height. Be careful with these calculations; precise measurements are key for accurate results! Frustums are practical shapes seen in everyday items like buckets or lampshades and knowing their volume helps in designing objects efficiently.
Also, Try our Arcsin Calculator to determine the arcsin (inverse sine) of a value.
Practical Applications of Cone Volume
Exploring the practical uses of cone volume calculations reveals a world where geometry meets reality—whether it’s ensuring the right quantity of ice cream fits into your sugar cone or determining how much concrete is needed for a traffic cone mold.
These applications are not only fascinating in their diversity but essential to various industries, showcasing the significance of understanding this fundamental geometric calculation in everyday life.
Finding The Volume Of a Cone-Shaped Container
To find the volume of a cone-shaped container, grab a tape measure and jot down the container’s height and radius. These are your key ingredients for the magic formula: one-third times pi times the radius squared times the height.
Just like making a cake, mix these numbers together to bake up your cone’s volume.
Imagine filling that cone with lemonade on a hot day. Knowing its volume lets you plan how much you can serve. Say goodbye to guessing games! With this formula, containers become crystal clear in their capacity – no surprises or overflow when pouring liquids or storing items.
Use it at home, school, or work, and watch efficiency pour out effortlessly!
Calculating The Amount Of Liquid In a Cone-Shaped Tank
Figuring out the liquid in a cone-shaped tank is simple with the right steps. You’ll use the formula V = (1/3)πr^2h. Here, V stands for volume, r is the radius at the tank’s base, and h is how tall the cone is.
Measure these two things – radius and height – then put them into this formula.
This process helps anyone needing to know how much liquid their conical container holds. It’s especially helpful for businesses that store or transport liquids in cones. They can manage resources well by knowing exactly how much fits inside their tanks. Unlock precise sphere calculations with our Sphere Calculator. Seamlessly compute dimensions for accurate results.
Step-by-step Guide On How To Use The Calculator
Calculating the volume of a cone is easy with a cone volume calculator. Here’s how to do it:
How to calculate the volume of a cone?
Calculating the volume of a cone doesn’t have to be hard. You just need the right formula and measurements.
- Choose the parameter you want to solve for, such as radius, volume, height, base area, slant height, surface area, and lateral surface.
- Enter the value of the radius into the calculator.
- Type in the height measurement.
- Press the calculate button to see your result.
- You will get the results.
Example
Let’s say you’re planning a party and want to fill a cone-shaped bag with candy. You have the bag which is 10 inches high and has a circular opening with a diameter of 6 inches. First, find the radius by dividing the diameter in half, giving you 3 inches for the radius.
Now use these numbers in your Cone Volume Calculator.
Enter “3” for the radius and “10” for the height into the calculator. Once you hit calculate, it tells you that this cone-shaped bag can hold about 94.2 cubic inches of candy! This info helps you figure out how much candy to buy so each bag is full.
Now that we’ve got plenty of sweet treats ready let’s look at some common questions people might have about cones and volumes.
FAQs
1. Can it calculate for shapes like a frustum too?
Absolutely! The calculator adjusts to find the frustum volume, which means you just need to know the top and bottom radii, alongside the height.
2. Is this calculator only for cones with circular bases?
No, it’s versatile—while it’s great for right circular cones, it can also handle calculations for conical frustums with different-shaped bases.
3. How does knowing the volume of a cylinder help me with cones?
Knowing cylinder volumes helps because a cone’s volume is one-third that of a cylinder with the same base and height. It gives you quick insight!
4. What if my cone isn’t standing straight up? Does that change things?
If your cone leans over—what we call an oblique cylinder—the formula gets more complicated, but our tool still gets you the right answer fast.
5. Are there any other fun facts about using this calculator?
Sure thing! You’ll discover how changing lengths affect volume and see firsthand how geometry connects objects like pyramids, cylinders, and spheres in amazing ways.
Related Calculators: