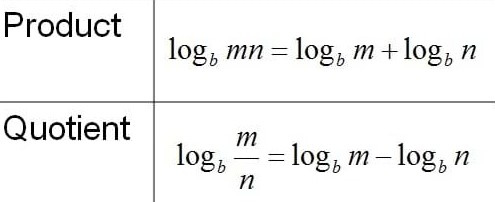Ensure accuracy and simplify your calculations by utilizing the Log Addition Calculator. It’s a user-friendly tool designed to make your log addition tasks effortless. Save time and avoid errors.
RESULTS
If you’ve ever grappled with logarithmic equations, you know that adding logs can be a difficult task. A log addition calculator is your ally in simplifying this complex process. This guide will help you in adding logs, guiding you through each step with clarity and ease.
What Is A Logarithm And How Is It Used?
A logarithm serves as the inverse function, crucial for unraveling the exponents linked to a given number. It’s a mathematical tool that simplifies complex problems across various fields by reducing multiplication and division to addition and subtraction.
Definition Of Logarithm
A logarithm is like a detective. It finds the missing number called an exponent that makes a certain value when you raise a base to it. For example, if you have 10^3 = 1000, the logarithm tells us that the exponent is 3 because 10 raised to the third power equals 1000.
Think of logs as shortcuts in math. They turn long multiplication problems into easier addition ones by using exponents. This trick comes in handy, especially with big numbers or solving for unknowns in equations.
Logarithms help us manage these tough tasks quickly and efficiently!
Common Uses In Mathematical Equations
Logarithms turn hard problems into easier ones. In math, they change difficult multiplication into simple addition. This is handy for solving exponential equations where numbers grow very fast.
Logs also divide turn into subtraction, which makes complex calculations much simpler.
They are key in science and engineering too. Logarithms help find out how quickly things like bacteria or money grow over time. With logs, you can solve real-world problems involving rapid changes easily and accurately.
Types Of Logarithms
Base 2, Base E, And Base 10
Base 2 logarithms are key in computer science. Computers use a language of zeros and ones, which is binary code. For this reason, base 2 logs help us understand data storage and processing.
Base e or natural logarithms pop up all over mathematics. They’re crucial for studying how things grow quickly, like bacteria, or shrink fast, like radioactive decay.
Logs with base 10 make our lives easier when dealing with big numbers or tiny ones. These logs can simplify complex calculations that involve powers of ten, making them handy for scientists and engineers alike.
Whether you’re calculating pH levels in chemistry or measuring earthquake intensity with the Richter scale, base 10 logarithms smooth out tough math problems. Enhance your mathematical precision with our Antilog Calculator. Effortlessly compute antilogarithms for accurate results.
How To Convert Between Different Bases
Converting between different bases is a key math skill. The change in the base formula makes this possible.
- You first need to understand the log function you’re working with. Let’s say you have log base 10 (log₁₀) and want to convert it to log base 2 (log₂).
- Use the change of base formula: This states that log base B (A) equals log base C (A) divided by log base C (B).
- Write down your number: If you need to convert log₁₀(100) to log₂, start by writing it out.
- Apply the change of base formula: It looks like this – new log = old log/conversion factor.
- Calculate using a calculator: For our example, this is log₂(100) / log₂(10).
- Simplify your answer: When you plug those numbers into a logarithmic equations calculator, you get your new base number.
- Practice these steps with different numbers and bases: The more you practice, the better you’ll understand how to switch between logarithmic bases.
Advantages of Using a Log Addition Calculator
Saves Time And Reduces Errors
Using a log addition calculator makes solving math problems faster. You spend less time on calculations and more time understanding the concepts. It’s like having a math expert by your side, giving you the right answers quickly.
This tool is great for homework, projects, or any task where you need exact numbers fast.
Mistakes can easily happen when adding logs by hand. A misplaced decimal or wrong base number can throw off an entire equation. With a log addition calculator, those slip-ups are less likely to happen.
It double-checks every step so that you get accurate results every time. This means you can trust the work you do and move forward with confidence.
Can Handle Complex Equations
Log addition calculators are a big help with tough math problems. They let you work out complicated logarithmic equations without making mistakes. You can solve tricky questions faster and more accurately than using pen and paper.
This is great for anyone tackling advanced math, whether in school or professional work.
These calculators make it simpler to focus on the ideas behind the equations. They take care of the hard number crunching for you. With this tool, complex tasks like solving for x or changing log bases become much easier to manage.
Now, imagine applying these calculations to real-world situations, it’s time we explore how logs are used in everyday life and various careers! Empower your mathematical prowess with our Factorial Calculator. Seamlessly compute factorials for accurate results.
Practical Applications of Logarithms
Logarithms play a vital role across various fields; from predicting the magnitude of earthquakes in seismology to calculating compound interest in finance, they form the backbone of many essential applications.
Mastery of logarithms opens up pathways to understanding and innovating within disciplines that shape our world, such as science, engineering, and economics.
Science And Engineering
In science and engineering, complex problems often involve exponents and exponential growth. Scientists and engineers use logarithms to break these big numbers into smaller, more manageable pieces.
This helps make sense of data that changes quickly or by huge amounts. For example, when measuring earthquakes with a seismograph, the Richter scale uses logarithms to turn tiny pen wiggles into meaningful measurements.
Logarithms also play a key role in designing circuits in electronics. They help engineers decide on resistances and currents for safe and efficient designs. These math tools are behind many discoveries and inventions we rely on every day.
With the help of log addition calculators, tricky calculations become simpler, letting experts focus on innovation rather than getting stuck in number crunching.
Finance And Economics
Just as logarithms are crucial in science and engineering for precise calculations, they play a vital role in finance and economics. They help us understand the complex world of money growth and investment decay.
With logarithms, economists can forecast how investments will perform over time. This understanding is key to making smart choices about where to put money.
Logarithms also shine when dealing with interest rates and the value of future money. Financial experts use them to find out what today’s savings could be worth years from now. And it’s not just about projections; these tools help manage risks too.
The Log Addition Calculator simplifies this process, letting users quickly see results without getting bogged down in numbers. It transforms tough equations into straightforward solutions, guiding financial planning one step at a time. Elevate your financial strategy with our Enterprise Value Calculator. Navigate business valuation effortlessly and make informed decisions.
Step-by-step Guide on How To Use A Calculator
Using our log addition calculator is easy and efficient. Here’s how you can quickly get the results you need:
- Look for the input field labeled “Enter Comma Separated Numbers.”
- Type in your first log value in this field.
- Add a comma, then input your second log value.
- If you have more values, keep adding them with commas in between.
- Now, find and press the “Calculate” button on your screen.
- The calculator will work fast and show you the sum of your logs.
- It will also display each calculation step in column 1 for clarity.
- In column 2, look at every step needed to solve the problem.
Examples
Now that you understand the steps, let’s look at some examples of solved problems using a logarithm calculator.
1. Solving log(2) + log(3):
- Enter log(2) and log(3) into the calculator.
- Hit the calculate button.
- The calculator shows the answer is log(6).
2. Figuring out log(10) + log(5):
- Type in log(10) and log(5).
- Click calculate.
- The result will be displayed as log(50).
3. Adding Multiple Logs:
- Put in log(4), log(8), and log(12).
- Press calculate.
- The calculator provides you with the sum, which is equal to log(384).
4. Combining Logs with Different Bases:
- Change the base of each logarithm to a common base if necessary.
- Input these values into the calculator.
- Get your combined logarithmic value after calculation.
Let’s work through an example using our log addition calculator. Imagine you have two logs you want to add: log base 2 of 8 and log base 2 of 16.
- First, enter the numbers separated by a comma into the calculator. In this case, you would type “8,16”.
- Next, select the base for the logarithms. For our example, choose base 2 from the options given.
- Press the calculate button to find the sum. The calculator will show you the combined result of adding these two logs.
- You’ll see the complete calculation in column one. This is where your answer is explained.
- Column two breaks down each step needed to solve this problem. Follow it if you want to understand how we got to the answer.
- Our results show that log base 2 of 8 plus log base 2 of 16 equals log base 2 of (8*16).
- That simplifies to log base 2 of 128, which equals 7 when calculated.
- The calculator proves that adding logs is like multiplying their inside numbers first before finding their single logarithm value.
FAQs
1. What logarithmic bases does the calculator support?
The Log Addition Calculator is versatile and supports logarithmic bases such as common logarithms (base 10), natural logarithms (base e), and other custom bases.
2. Can I use non-integer logarithmic values with this calculator?
Yes, the calculator supports both integer and non-integer logarithmic values. Just input the values correctly, and the calculator will provide an accurate result.
3. Is there a limit to the size of numbers I can input?
The Log Addition Calculator is designed to handle a wide range of logarithmic values, but extremely large or small values may result in numerical precision limitations. Exercise caution when working with very large or very small numbers.
4. Can I use this calculator for subtraction as well?
No, the Log Addition Calculator is specifically designed for adding logarithmic values. For subtraction, you would need a different tool or manually convert the subtraction operation into an addition operation using logarithmic properties.
5. Can I use Symbolab Pro for log addition calculations?
Yes, Symbolab Pro offers advanced features that make it easy to solve problems with exponents and exponential functions, including log additions.
6. Does a log addition calculator only work with simple numbers?
Not at all, this handy tool also manages matrices like matrices when adding logs, so you can tackle more detailed math challenges without trouble.
Related Calculators: