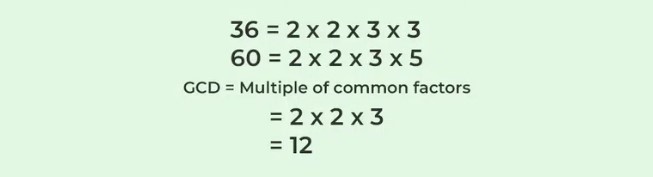Calculate with ease using our GCD Calculator! Simplify your mathematical tasks effortlessly and get accurate results in no time. Start now for a simple calculating experience.
RESULTS
Struggling to simplify fractions or find common factors in your math problems? The Greatest Common Divisor (GCD) is a key concept that can unlock these challenges with ease. Our guide will walk you through the steps of using a GCD calculator effectively, ensuring you get accurate results quickly and stress free.
Understanding GCD
It’s all about finding that largest number which can divide a set of integers without leaving any remainder.
By mastering this concept, not only do we simplify fractions and solve problems in arithmetic and algebra with greater ease, but we also lay the groundwork for more advanced computational methods.
Definition And Purpose
The greatest common divisor (GCD) is the biggest number that both of your numbers can be divided by without leaving leftovers. It’s like finding the biggest piece you could cut from two different ropes without any rope going to waste.
Knowing GCD helps simplify fractions and solve puzzles in math, helping everything fit together neatly.
Think of GCD as a tool for cleaning up maths problems. When you have it, reducing fractions becomes a breeze, and comparing ratios gets simpler too! It’s not just about making numbers look pretty; it often unlocks clues for bigger questions in mathematics and computing. Unlock mathematical precision with our Factorial Calculator. Seamlessly calculate factorials for precise results.
How To Calculate GCD
Calculating the GCD, or greatest common divisor, of two numbers means finding the biggest number that both numbers can be divided by without leaving a remainder. Start by listing all the factors of each number.
Look at these lists and pick out the largest number that appears in both. This is your GCD.
You have another way to do it: prime factorization. Break down each number into its prime factors, the prime numbers that multiply together to give you the original number. Compare these breakdowns and find all the matching primes between them.
Multiply these shared primes together to get your GCD.
Keep dividing the larger number by the smaller one until you reach zero as a remainder. The last divisor you used is your GCD.
Remember, tools like our online calculators are ready to help too. They’re great for quick answers, especially when dealing with more than two numbers or really large ones! Experience mathematical precision with our Octal Math Calculator. Simplify complex calculations effortlessly.
Greatest Common Factor (GCF) Calculator
When dealing with numbers, identifying the Greatest Common Factor (GCF) is crucial for simplifying fractions and understanding divisibility. The GCF calculator emerges as a brilliant tool to effortlessly calculate this important mathematical figure.
How To Find GCD
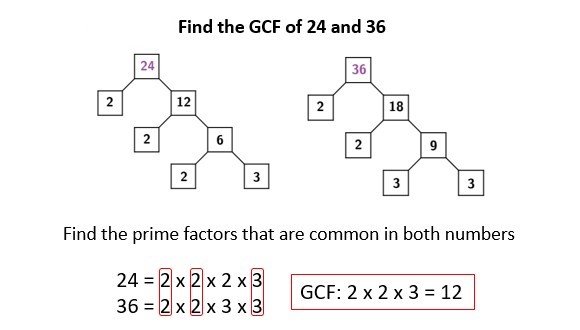
Using Factoring
Imagine you want to find the greatest common divisor of two numbers. Factoring is your tool for this job. You break each number into its prime factors, which are the building blocks of every number.
These are numbers that only divide by themselves and one.
Let’s say you have 20 and 30. Break them down into primes: 20 is made of 2 times 2 times 5, while 30 breaks down to 2 times 3 times 5. Compare these prime factors to see which ones they share.
Both have a 2 and a five in common! Multiply these together, what do you get? The GCD: it’s ten for both numbers!
Using factoring with a GCD calculator speeds things up, especially with big numbers that take longer to factor by hand. Just type in your numbers, hit calculate, and let technology do the tricky math for you! Keep your work accurate and efficient with this handy method; it simplifies fractions, helps solve problems in algebra, and much more.
Using Prime Factorization
Moving beyond basic factoring, prime factorization dives deeper into the structure of numbers. Break down each number into its prime factors, these are the building blocks that only divide by one and themselves.
Write out all their primes, then circle what they have in common. Multiply these shared primes together and you’ve found your GCD! It’s like uncovering a numerical puzzle where every piece fits perfectly.
This method shines when dealing with hefty numbers. Instead of trying random guesses to find divisors, lay down all the prime pieces on the table. With everything in plain sight, spotting common factors becomes a breeze! You’ll grasp how powerful this tactic is once you use it, especially for large figures that could otherwise take ages to solve by hand.
Online GCD calculators use this smart approach too; just type in your numbers and watch as they swiftly compute the greatest common divisor for you through prime factorization magic!
Using Euclid’s Algorithm
To find the greatest common divisor using Euclid’s algorithm, start by dividing the larger number by the smaller one. Write down the remainder. Now, take that smaller number and divide it by this new remainder.
Keep repeating this process: divide, get a remainder, and then use that remainder to divide again. You’ll continue until you hit a remainder of zero.
Look back at your last division where the remainder wasn’t zero. That number is your GCD! This method has been trusted for centuries because it’s reliable and works every time. If math isn’t your thing or you’re short on time, don’t worry, many online tools can do these steps for you in seconds.
Just type in two numbers and let the calculator handle the Euclidean divisions; it will spit out your GCD without any hassle. Unleash precision in your logarithmic calculations with our Antilog Calculator. Effortlessly compute antilogarithms for accurate results.
Difference Between GCD And HCF
GCD, or Greatest Common Divisor, and HCF, Highest Common Factor, are two names for the same thing. They both find the largest number that can be divided into a set of numbers without leaving a remainder.
People use GCD when talking about just two numbers. For more than two numbers, they often say HCF. But in truth, whether you call it GCD or HCF doesn’t change how you find it. The process is the same look for the biggest number all your original numbers share as a factor.
Knowing this helps us move on to calculators designed to do the math for us. It’s easy, you enter your numbers and get quick results showing what those common divisors are! Now let’s see how exactly these calculators make things simpler in our next step by step guide.
Step by step Guide On How To Use The Calculator
- Type your numbers into the “Enter Space Separated Value” box. Make sure there’s a space between each number you’re using to find the GCD.
- After entering them, click on “Calculate.” The calculator will quickly do the math and show you the greatest common divisor (GCD).
- You’ll also see other helpful details like common multiples, and for more complex problems, a complete detailed solution. This tool makes finding the GCD simple and fast, so you can understand your math problems better in no time!
Example
After hitting the calculate button, let’s say you entered 48 and 180. The calculator works its magic fast. It shows the GCD is 12, which means 12 is the biggest number that can divide both without leaving any leftovers.
You’ll also see listed common multiples and a step by step breakdown of how it found the answer. This way, you learn while you use it!
Imagine you’re baking cookies for your friends but have to share them equally. Think of the calculator as a recipe that helps make sure everyone gets the same amount without breaking any cookies apart.
Just pop your numbers in, press calculate, and share away with no crumbles left behind! Enhance your mathematical prowess with our Log Addition Calculator. Streamline complex calculations effortlessly.
FAQs
1. Is there another name for the Greatest Common Divisor?
Yes, the Greatest Common Divisor is also known as the highest common factor (HCF) or greatest common measure.
2. How can I find the GCD of two numbers?
You can find the GCD by breaking down each number into its prime factorizations and then multiplying together the smallest powers of all common factors.
3. What are coprime numbers?
Coprime numbers are a pair or set of numbers that have no other common divisors except 1; their GCD is always 1, making them a unique coprime set.
4. Does computing complexity matter when using a GCD calculator?
When you use a GCD calculator to find divisibility results, it manages computation complexity efficiently and gives you answers quickly and accurately.
Related Calculators: