Our dedicated slope calculator will help you find the slope (m) or the gradient between two points. All you have to do is follow the instructions mentioned on the calculator!
RESULTS
Understanding Slope and Its Significance
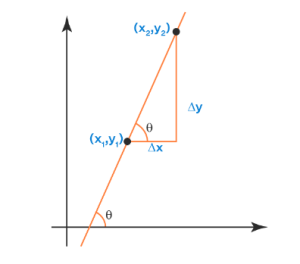
The slope of a line is the change in the y coordinate with respect to the change in the x coordinate.
Formula:
m = change in y/change in x = Δy/Δx
- m is the slope
- net change in the y-coordinate is represented by Δy
- net change in the x-coordinate is represented by Δx
Additionally, the slope of a line can also be represented by: tan θ = Δy/Δx (tan θ is the slope of a line)
Different Types Of Slopes
There are four different types of slopes, which are detailed here:
| Slope Type | Description | Formula | Example |
|---|---|---|---|
| Positive Slope | The line rises from left to right. | \(m > 0\) | \(y = 2x + 3\) |
| Negative Slope | The line falls from left to right. | \(m < 0\) | \(y = -4x + 2\) |
| Zero Slope | The line is horizontal. | \(m = 0\) | \(y = 5\) |
| Undefined Slope | The line is vertical. | The denominator of the slope is zero. | \(x = 4\) |
Overview Of Slope In Mathematical Analysis
A slope is like a ladder’s angle against a wall. It tells you how much a line tilts up or down in math. Think about climbing hills: A steep hill has a high slope, and a gentle hill has a low slope. In maths, we use the slope to see how things change together. For example, if you know how fast you walk and the time it takes to reach somewhere, you can find out how far away your destination is.
The formula for finding the slope uses two points on a straight line. You take the difference in their y-coordinates and divide it by the difference in their x-coordinates. This gives you the rate of change or slope of that line.
The steeper the line, the bigger this number gets. If lines go up from left to right they have positive slopes; if they go down they have negative slopes. Slopes help us predict things and solve problems in fields like science and engineering where understanding rates of change is key!
Explanation Of Slope Formulas
Now that you know how important slope is, let’s talk about how we find it. Finding the slope of a line means figuring out how steep it is. Picture walking up a hill; the steeper the hill, the harder you work to climb it.
In math, we measure this “steepness” with numbers.
Here’s one way to calculate slope: take two points on a line and look at their x and y values (these are just places on the graph). Subtract the y value of one point from the other and do the same for x.
This gives us two numbers. We call these differences numerators and denominators. Then we divide them – numerators over denominators – which gives us what we call ‘the rise over run‘.
The bigger this number, the steeper your line.
If you have ever seen an equation like “y = mx + b”, that’s called slope-intercept form. Here, m represents our slope—the thing we talked about as being like climbing a hill—and b is where our line starts off when x equals zero on our graph or what some people would call ‘crossing’ the y-axis.
Calculating slopes isn’t only for straight lines; sometimes curves in graphs go up and down, not just straight across – those are non-linear functions! And if someone throws words like hypotenuse or Pythagorean theorem at you while talking about slopes—don’t worry! Those come into play when dealing with right triangles found in more advanced problems involving distance and angles on graphs.
Remember, knowing these formulas helps make sense of things around us everywhere—from ramps to mountainsides to even roller coaster tracks!
Step-By-Step Guide For Calculating The Equation Of A Line
Calculating the equation of a line can seem tough, but with this guide, you’ll learn how to do it step by step. We’ll use slope formulas and simple math to find the right line equation from two points.
- First, write down the coordinates of your two points (x1, y1) and (x2, y2).
- Next, subtract y2 from y1 to get the change in y or Δy.
- Subtract x2 from x1 to get the change in x or Δx.
- Use these changes to find the slope (m). Divide Δy by Δx (m = Δy / Δx).
- The slope shows how steep the line is. A bigger slope means a steeper line.
- With the slope (m), choose one point (x1, y1) for the next steps.
- Get ready to use the point-slope form: y – y1 = m(x – x1).
- Plug in your point’s values and m into this formula.
- Multiply m with (x – x1) to simplify things.
- Add y1 to move it over to the other side of your equation.
- Take note of your two points
- Calculate changes in y and x
- Find your slope by dividing those changes
- Use a single point with your slope in point-slope form
- Simplify your formula
Features Of The Slope Calculator
The Slope Calculator empowers students to effortlessly conquer the complexities of slope calculations, offering a robust array of functionalities designed to handle various input data with precision.
From exploring different methods of computing slopes to delving into related concepts like y-intercept and angle measurements, this tool is engineered for comprehensive analytical support.
Input Parameters And Values
Slope calculators are helpful tools for math. They let you find the slope of a line easily. Here’s how you put information into a slope calculator:
- You can use whole numbers, fractions, or mixed numbers.
- For two points, enter the x and y coordinates like (2,3) and (4,5).
- If you know one point and the slope, just type them in.
- Want to use distance? Put in one point with the slope and how far it goes.
- To find out about x or y alone, input one point with the slope and either the x or y value.
- Just have a line’s equation? Enter it to get the slope.
Different Calculation Methods
Calculating slope is important in math. It helps us understand how steep a line is. Here are some ways you can figure out the slope with a calculator:
- Two Points: You need two points for this method. Each point has an “x” and a “y” value, like (x1, y1) and (x2, y2). The calculator finds the vertical change (ΔY) and horizontal change (ΔX) between them. Then it uses the slope formula: (y2 – y1) / (x2 – x1). This gives you the slope of the line.
- One Point with Slope (m) & Distance: If you have one point and know the slope and how far another point is from it, use this method. Give your points “x” and “y”, type in the slope (m), and add the distance. The calculator will show you where the second point is.
- One Point with Slope (m) & X or Y: Here, start with one point and the slope again. But this time, only add either a new “x” value or a new “y” value. This will help you find another point on that same line.
- One Point & Slope (m): Have just one point? That’s okay! Type in its “x” and “y” values along with the slope (m). The calculator then makes an equation of a line in slope-intercept form: y = mx + b.
- A Line: Sometimes, you might already have an equation of a line like y = mx + b. Just put that into the calculator! It will tell you about the line’s steepness and where it crosses the y-axis.
Additional Options For Y-Intercept And Angle Calculation
The slope calculator is a handy tool for math students. It not only finds the slope but also calculates the y-intercept and angle of a line.
- Use two points on a line to find the slope. This method shows how steep the line is.
- Find out where your line crosses the y-axis. The calculator will give you this point, called the y-intercept.
- Learn about the angle your line makes with the x-axis. The calculator tells you this in degrees.
- Input one point and the slope (m). With these, you’ll see where your line goes and its steepness.
- Calculate the midpoint between two points using the midpoint calculator option.
- If you have a vertical line, know that it has an undefined slope. The calculator will tell you so because dividing by zero doesn’t work in math.
- For horizontal lines, get comfortable knowing they have a zero slope. It’s like a flat road without any hills.
How To Use The Slope Calculator
4. How to Use the Slope Calculator: Discovering the simplicity of slope calculations is just a few clicks away, as we guide you through inputting data and interpreting the precise results our tool provides—empowering your mathematical journey with confidence and clarity.
Input Options And Output Results
A slope calculator helps you find the steepness of a line. It’s easy to use and gives you quick answers. Here’s what you can do with it:
- Choose how you want to find the slope. You can use two points, one point and the slope & distance, or other ways.
- Type in the numbers you know. These could be whole numbers, fractions, or mixed numbers.
- Press enter and see your results right away. The calculator tells you many things like:
- Slope (m): This is your main answer and shows how steep the line is.
- Percentage grade: It tells you the slope as a percentage.
- Angle (θ): This shares the tilt of the line in degrees.
- Distance: Find out how long the line is between points.
- ΔX and ΔY: These show how much x and y change between your two points.
- X-Intercept: Learn where the line crosses the x-axis.
- Y-Intercept: See where it crosses the y-axis on your graph.
Examples For Each Calculation Method
Slope calculators are handy tools for students learning about lines and angles. They make finding slopes quick and easy. Here are some ways to use different methods on the slope calculator:
- Two Points:
- Enter the x and y coordinates of two points.
- The calculator will show the slope (m), distance, ΔX (change in x), ΔY (change in y), and the equation of the line.
- One Point with Slope (m) & Distance:
- Type in one point’s x and y values.
- Add the slope value (m) and the distance from the point.
- Results will include a second point that creates this slope at that distance.
- One Point with Slope (m) & X or Y:
- Put in an x or y coordinate along with the slope value (m).
- The calculator figures out the other point needed to achieve this slope.
- One Point & Slope (m):
- Input one point’s coordinates.
- Provide the value for slope (m).
- Get results for what line passes through this point at this angle, including its equation.
- Line Calculation:
- Give any line’s equation.
- Find out its rise over run, which is another way to say its slope.
FAQs
Question: How Does A Slope Calculator Use Point-Slope Form?
The slope calculator uses point slope form to create an equation from one point and the slope, helping you understand how lines go up or down on a graph.
Question: Can I Use The Pythagorean Theorem With A Slope Calculator?
Yes, you can use the Pythagorean theorem in some cases with your slop calculations to find distances when working with right triangles and altitude.
Question: What Happens If I Try Dividing By Zero In A Slope Calculation?
In math, division by zero isn’t allowed because it doesn’t make sense—it means you’re trying to split something into zero parts! A good rule is to remember: that we can’t divide by zero.
Question: Does Differential Calculus Relate To Finding Slopes Of Curves Rather Than Straight Lines?
Yes, differential calculus involves differentiating polynomials and other functions to find out things like curvature—how curvy or bendy—a curve is instead of just looking at straight lines.